歩行・交通振動・風などが原因で、床や建物が大きく揺れることがありますが、これは「共振」という現象であることが多いのです。
今回はこの「共振」についてわかりやすく解説します。
固有振動数とは
共振を理解するためには、まず固有振動数について説明する必要があります。物体にはそれぞれ固有の揺れやすい振動数（1秒間に振動する回数）があり、この振動数を「固有振動数」と呼びます。
ある物体にたたくような力を加えると、その直後から固有振動数の揺れが発生します。固有振動数は物体の形状や物性値によって変わります。例えば、ピアノなどの弦楽器は弦の長さ（ℓ）や張りの強さ（S）によって固有振動数が決まり、弦をたたくとその固有振動数で振動し、音が鳴ります。
参考までに、弦の固有振動数を計算式で表します。
ｆ = 1
2ℓ√S
ρ
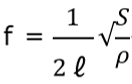
- ｆ：固有振動数 Hz （1秒間に振動する回数）
- ℓ：弦の長さ ｍ
- S：張力 Ｎ （弦を引っ張る力）
- ρ：線密度kg/m （弦の1ｍあたりの重さ）
この関係から分かるように、ピアノなどは弦の長さと張力を調整することで固有振動数を変化させ、ドレミの音階を表現しています。
共振とは
共振とは、外部からある物体に固有振動数に等しい（近しい）振動が入力されて揺れが大きく増大する現象のことを指します。例えば、歩道橋で、歩行（外部からの入力）のテンポが固有振動数と一致すると、一人が歩いただけで揺れを感じることがあるように、比較的小さい力でも大きな揺れを引き起こすことがあります。
ちなみに、振動ではなく音が共振する場合は、共鳴と言います。
共振曲線の意味
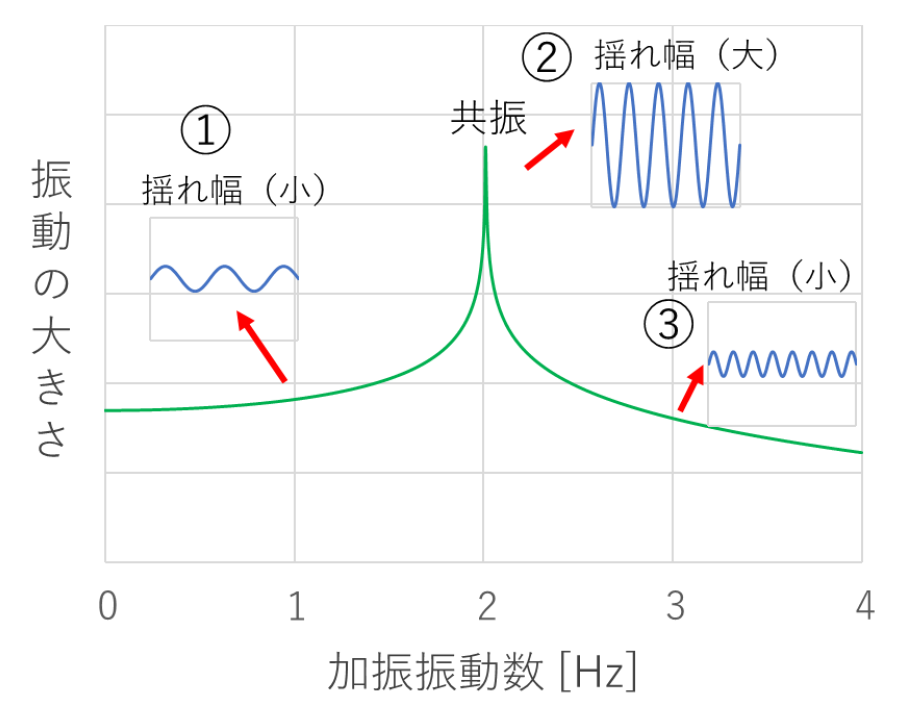
ある物体の固有振動数が2Hz（1秒間で2回の振動）の場合、入力される振動の振動数（Hz）と発生する振動の揺れの大きさの関係を表すと図1のような共振曲線になります。
加振振動数が固有振動数（2Hz）に近づくと揺れは大きくなり、固有振動数で最大になります。さらに加振振動数が固有振動数から離れるにつれて、揺れが小さくなっていきます。
図1 共振曲線
共振による振動増大を防ぐ方法
小さい力でも大きな振動を引き起こす共振現象は、時に居住性能（快適性）を悪化させ、大きな問題になります。これを防ぐには、いくつかの方法があります。
歩行による床の揺れで共振が起きた場合を例に挙げます。
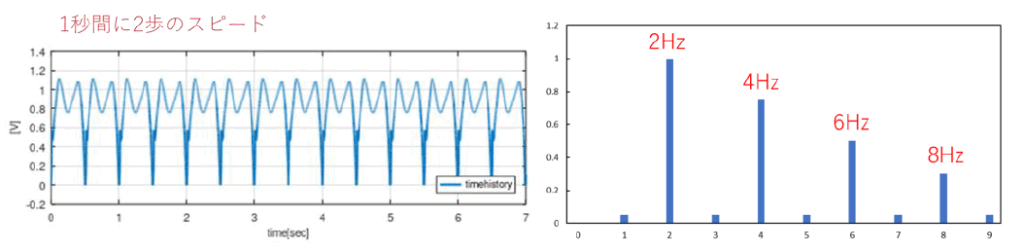
例えば、歩行のテンポが1秒間に2歩（2Hz）であると仮定した場合、振動数2、4、6Hzなどの2Hzの整数倍に加振力成分を持つ力が床に入力されます（図2）。床の固有振動数とこれらの加振力成分が一致すると、床が共振し揺れが大きく増大します。
図2 歩行によって床に入力される力
この場合、共振を防ぐ代表的な対策は2つあります。1つ目は、加振周波数と床の固有振動数を一致させない（共振させない）ことです。2つ目は、共振による揺れの増大を抑える方法です。
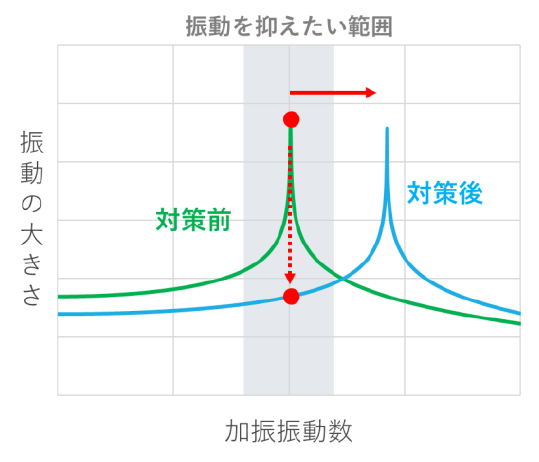
1つ目の具体的な対策として、床の固有振動数を上げて、歩行の加振周波数とずらして共振を避ける方法があります（図3）。これは、梁を大きくしたり、小梁の数を増やすことで、構造体の剛性を増し固有振動数を上げる方法です。
ちなみに、床の固有振動数を下げる方法でも、共振を避けることができます。ただし、床の固有振動数を下げる方法は、床を華奢に（揺れやすく）することになるため、共振を避けても揺れ自体は大きくなる可能性があり、あまり良い方法とは言えません。
図3 固有振動数を上げることで共振させない対策
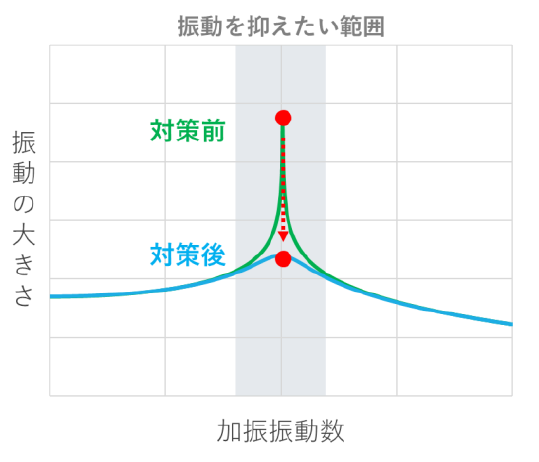
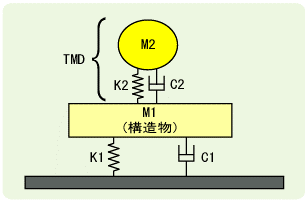
2つ目の対策は、減衰を付加することで、共振による揺れの増幅を小さくして揺れを抑える方法です（図4）。具体的には、制振装置と呼ばれるTMD（Tuned Mass Damper）やAMD（Active Mass Damper）を床に設置し、床の揺れを吸収するように制振装置の錘を揺らすことで、共振による揺れの増大を抑えることができます（図5）。
図4 減衰を付加することで共振による揺れの増大を抑える対策
図5 床に取り付ける制振装置のモデル