前回の豆知識 振動・騒音分析基礎(1)ではオクターブ分析について説明しました。今回はもう一つの代表的な周波数分析の手法であるFFT分析について、わかりやすくまとめました。
FFT分析とは
FFT分析のFFTとはFast Fourier Transform:高速フーリエ変換の略です。高速とついていることからわかるように、フーリエ変換を効率的に早く行う手法です。ではフーリエ変換とはどういうものでしょうか?実際の音や振動は大きさの異なる単純な波形(いろいろな周波数のサイン波)が重なり合って複雑な波形を作っていると考えることができます。この複雑な波形を単純な波形に分けてどの周波数成分がどのくらい含まれているかわかる状態にすることをフーリエ変換といいます。実際に私たちの日常で現れる振動は時間軸でみると図1のように複雑な振動波形をしていますが、これらは単純な振動波形を足し合わせたと考えることができます。図2は図1の複雑な振動波形をFFT変換した結果です。横軸が時間軸から周波数軸に変わっています。複雑な振動波形をFFT変換すると3Hz、9Hz、20Hzの周波数成分の振動があり、中でも3Hzの成分の振動が最も(振幅が)大きいことがわかります。
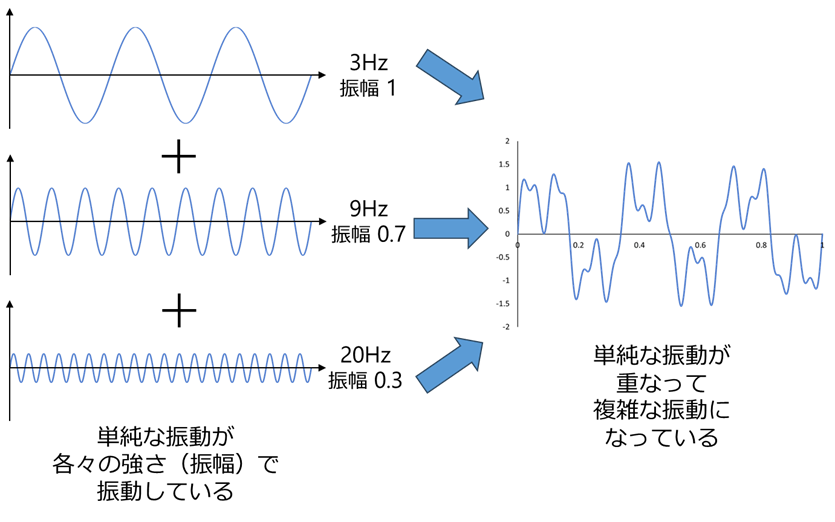
図1 複雑な振動波形とその構成振動波形
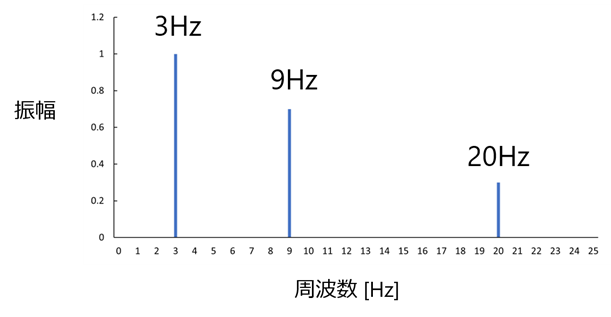
図2 複雑な振動波形をFFT変換した周波数のグラフ
また、フーリエ変換の概念をまとめると図3のようになります。時間軸で見ていた振動波形を周波数軸側という別の軸で見るというイメージです。
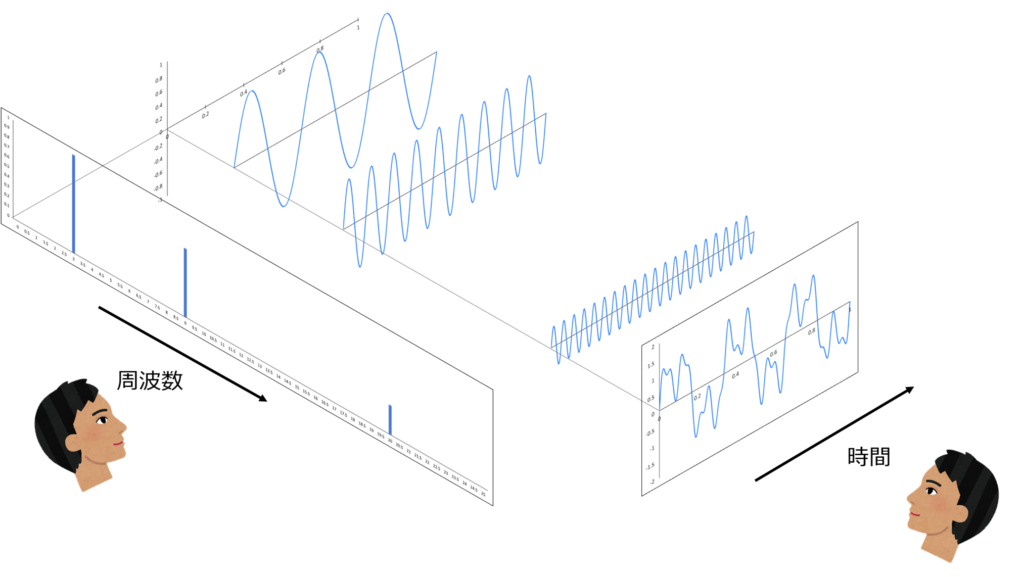
図3 フーリエ変換の概念図
オクターブ分析が31.5Hz、63Hz、125Hzのように間隔が1オクターブごとの等比間隔の周波数軸に対し、FFT分析では、周波数軸が等間隔でかつ細かい幅で分析されるのが一般的です。従って、FFT分析の方が周波数軸に対して、細かい分析が可能になります。そのため、固有振動数の測定や伝達率の測定などの周波数ごとの大きさの違いを細かく見たい場合に用いられます。他にも、工場の生産ラインにて発生振動の周波数や大きさを記録しておき、軸受けなどに損傷が出ると、振動の大きい周波数が変化したり、大きさが変わるなどの異常事態の検出に用いたり、メンテナンスの時期を決めるのに用いられます。一方のオクターブ分析は周波数間隔は大きいですが、人の感覚とよく合う分析方法なので、音の分野ではオクターブ分析もよく用いられます。
実際の振動分析の例
実際にヤクモが振動を測定し、FFT分析した例を紹介します。
事務所内での歩行によって床が大きく揺れてしまう問題を対策した事例です。図4は人が歩行しているときの振動波形です。加速度振幅で2~3cm/s2の揺れが発生しています。図5の灰色線はこの波形をFFT分析(高速フーリエ変換)した結果で、7.5Hzにピークがあります。7.5Hzで2~3cm/s2程度の揺れというのは、フワフワした感じがやや気になるという大きさの揺れで、居住者が感じていたのはこの成分の振動であると考えららます。また、事前の調査でこの床の固有振動数も同じく7.5Hzであることがわかっていたので、歩行時に発生している大きな揺れの正体は、床の共振現象であると判断できます。従って、この問題を解決するためには、床の共振増幅をおさえる必要があります。
そこで制振装置AMD(詳しくはコチラ)を用いて7.5Hz成分を下げる対策を行いました。図5の青線が対策後の結果です。対策前の7.5Hzの鋭いピーク(灰色線)が無くなっています。図6の対策後の歩行しているときの振動波形を見ると加速度が0.5cm/s2となり、床揺れを1/4に低減できました。
AMDなどの制振対策はピークの周波数や共振周波数をより正確に知ることが重要ですので、細かく周波数分析できるFFT分析が有効です。
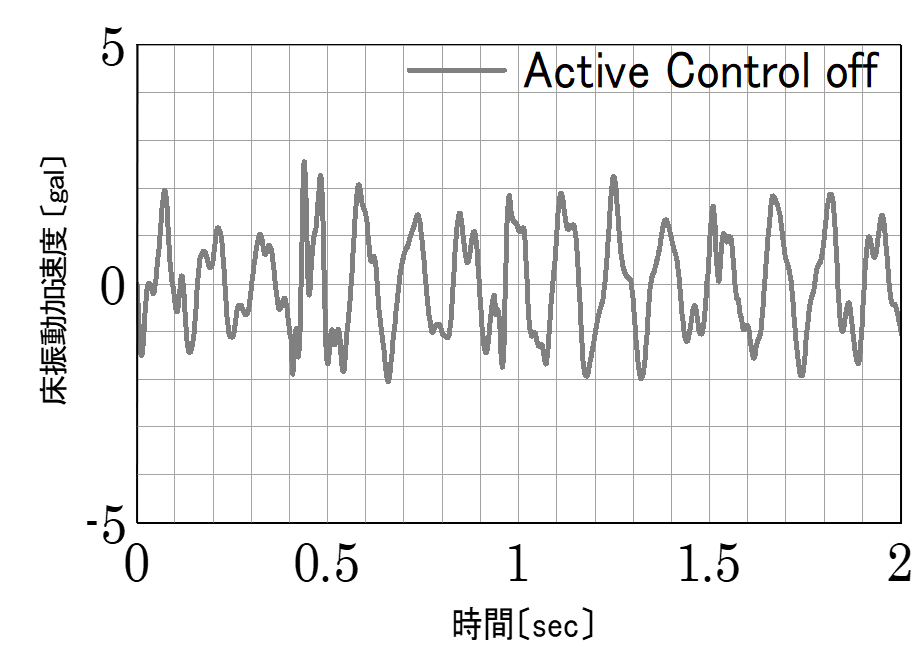
図4 対策前の振動波形
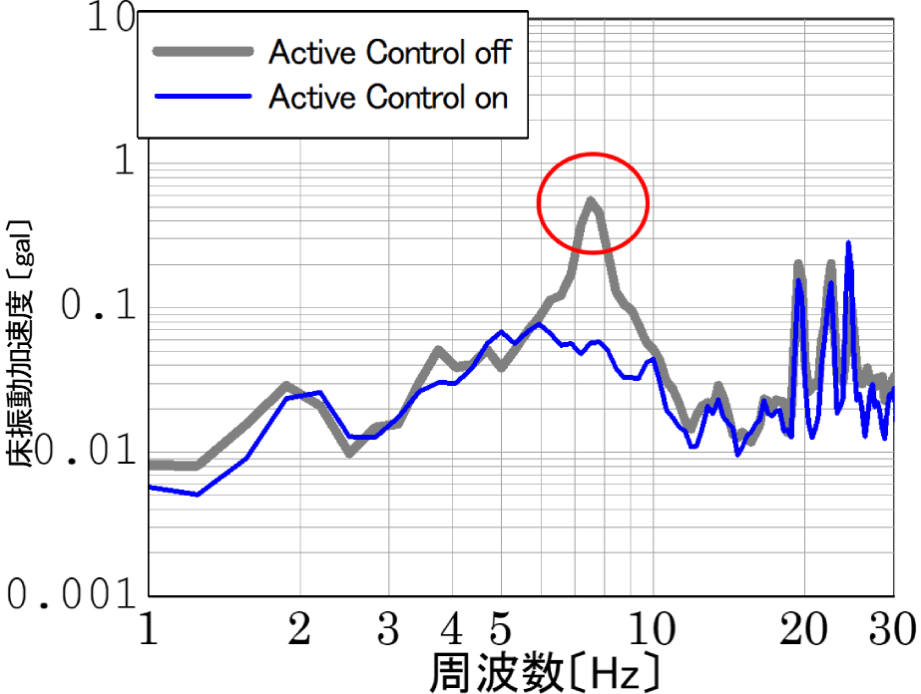
図5 周波数分析の結果
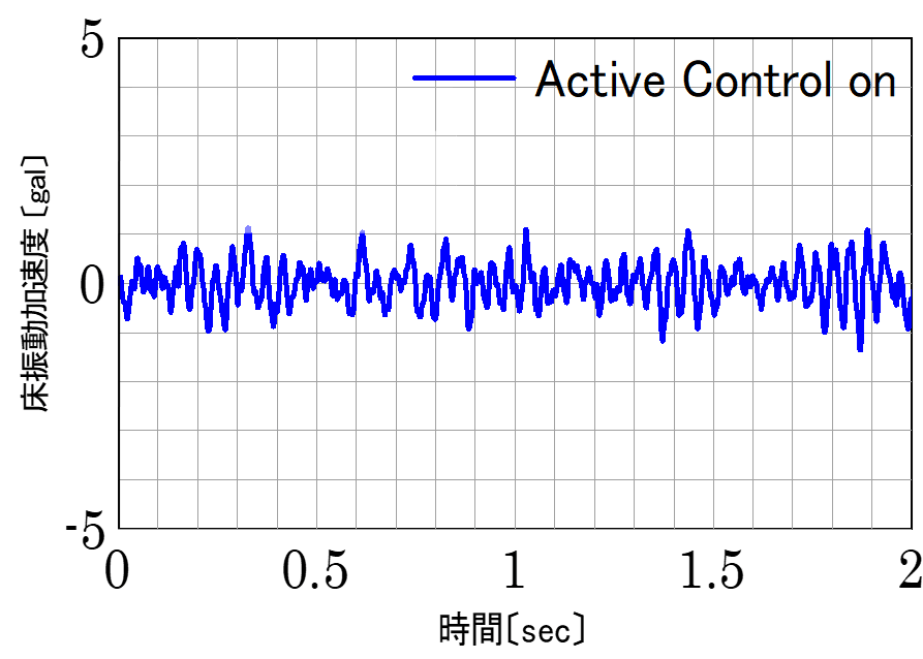
図6 対策後の振動波形
