The dB (decibel) is a unit widely used to describe the intensity of sound and vibration. In this trivia, we will explain the basic concept of the decibel and how it is used in actual measurements in an easy-to-understand manner.
What is dB (decibel)?
The "bell (B)" in dB is the name given to a dimensionless quantity expressed as the ordinary logarithm of the ratio of a reference quantity to a physical quantity, which the British-born American inventor Alexander Graham Bell is said to have used to describe the power transmission attenuation of a telephone.
"Deci (d)" is a prefix of SI units (10)-1and when the ratio of quantities is a general factor of magnification, such as 2 or 10 times, the value was multiplied by 10 for convenience because of handling problems such as small solutions with the bell (B), and thus the decibel (dB) (decibel).
dB (decibel) is "10 times the ordinary logarithm of the ratio of two powers." It is the ratio of the power of the target to the power of the reference, one being the reference power and the other the target power, quantified using the ordinary logarithm.
As an example, if the reference quantity is X0the physical quantity is X, and the ratio of X to X0is expressed in dB (L), the following formula is used.
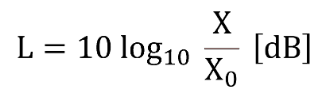
What is vibration acceleration level?
When vibration is expressed in dB, the physical quantity is the square of the acceleration rms value of the vibration.
The above shows the acceleration rms value of vibration as A[m/s2], the following equation is used. where VAL is called the vibration acceleration level.
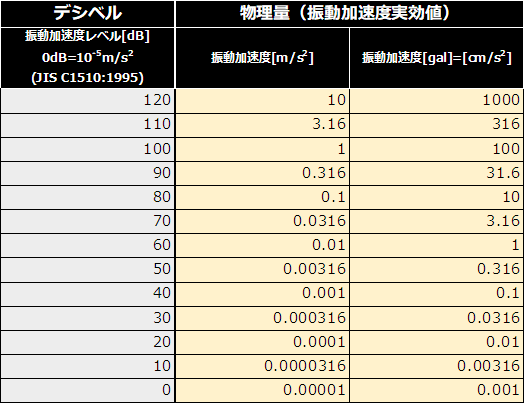
In the area of vibration related to building habitability, along with these decibel values, the physical quantity of vibration acceleration ([m/s2], [gal]) are also often used. Therefore, Table 1 below shows the vibration acceleration level [dB] and the vibration acceleration physical quantity ([m/s2], [gal]), and a contrast table showing the relationship between the two.
Table 1 Decibel-physical quantity contrast table for vibration
Contracted research and consulting services related to soundIn the following section, vibration acceleration levels are also used to make measurements.
What is sound pressure level?
When sound is expressed in dB, the square of the sound pressure RMS value is used for the physical quantity.
When the effective value of sound pressure is p[Pa], it is expressed by the following equation. where Lpis called the sound pressure level.
Contracted research and consulting services related to soundIn the following section, the sound pressure level is used to make measurements.
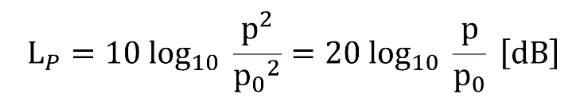
Reason for expressing in dB (decibel)
The range of sound and vibration intensity (magnitude) around us is so wide that it is difficult to handle very small to large numbers. By expressing this wide range of numbers in levels using dB, the data becomes easier to handle. Another reason is that dB-ized numbers are proportional to human senses.
References
New Pollution Prevention Technology and Laws 2025 Noise and Vibration Edition Edited by Pollution Prevention Technology and Laws Editorial Committee