Octave analysis is often used to evaluate vibration and sound. What is an octave anyway? What is octave analysis? This presentation will explain in an easy-to-understand manner...
What is octave?
You have probably heard the word “octave” in octave analysis in music talk. In Western music, the eight pitches from the lowest Do to the next higher Do are called an octave. The first Do is 261 Hz (Hz: number of vibrations per second), the next Do is 522 Hz, and the relationship between these two notes is called an octave.
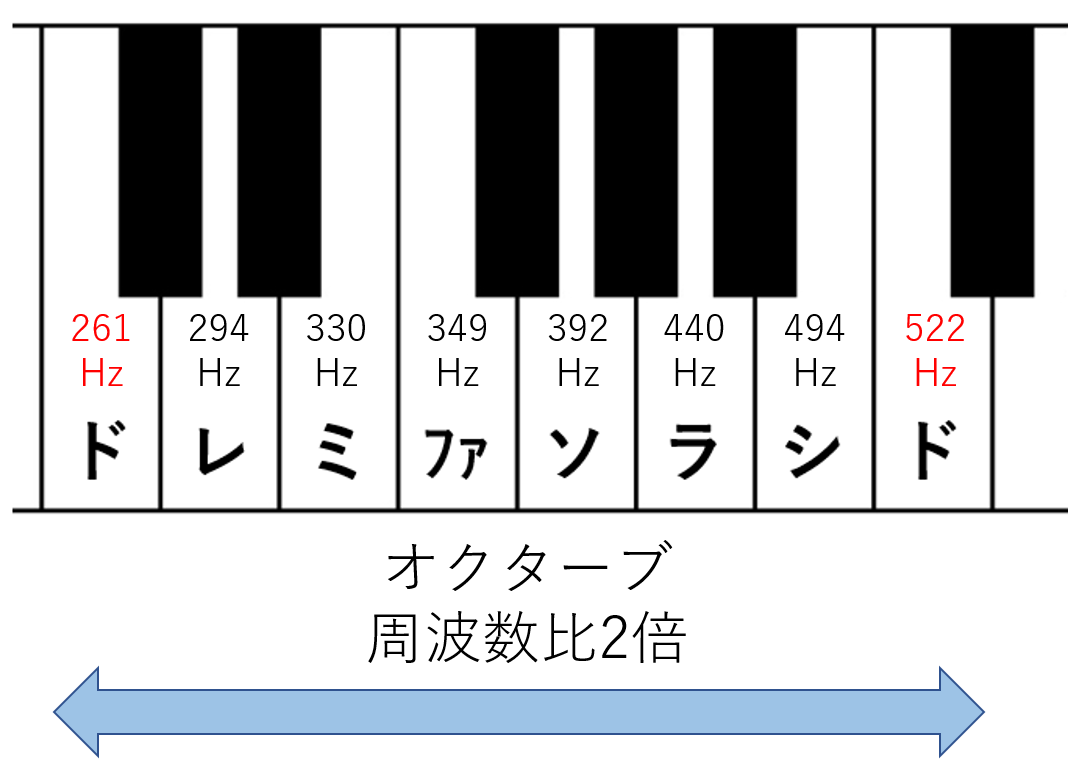
Figure 1 Relationship between piano keys and octaves
What is Octave Analysis?
Octave analysis is a method of analyzing the magnitude of sound or vibration at each frequency. To illustrate with sound, the sounds we normally hear are made up of a mixture of sounds of various frequency components. By dividing these sounds into appropriate frequency bands, we can understand the frequency characteristics of sound. Why analyze each frequency band separately? The reason why it is necessary to analyze each frequency band is that the all pass sound pressure level (A characteristic sound pressure level: the sound pressure level corrected for human hearing characteristics), which is the loudness of all frequency components, is used in general sound evaluations such as noise control laws, as shown in Figure 2.
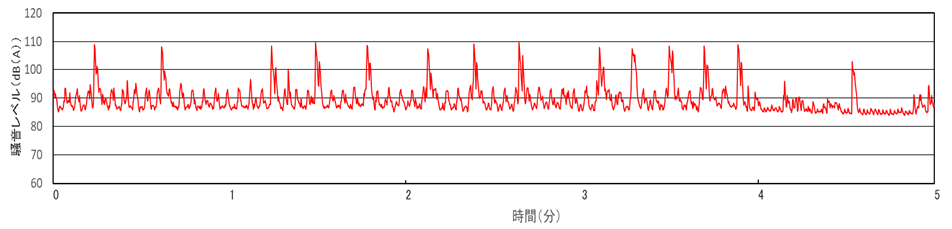
Figure 2 Time history analysis of noise levels
This data is very easy to understand to get a trend of the maximum value of noise, timing of noise, and intervals, and this is not a problem if you just want to evaluate the audible loudness of the sound. However, when considering measures to reduce this sound, it is necessary to identify which frequency components are louder. This is because if the sound level is loud in the low frequency component, the sound will not be reduced even if effective noise reduction measures are applied to the high frequency component. Therefore, it is necessary to take optimal noise reduction measures according to the frequency band of the problematic sound, so the analysis with frequency as the horizontal axis, such as octave band analysis, is considered to be effective.
Octave analysis, like time history analysis, is an analysis method that checks the maximum, minimum, average or time rate noise level (the noise levels during the measurement time are sorted in order of loudest to loudest to see what percentage of the total the loudness corresponds to. It is used as an evaluation method for noise and vibration control laws.) can be analyzed for each octave band.
Octave band range
Typical center frequencies used in octave analysis are 31.5 Hz, 63 Hz, 125 Hz...8 kHz for sound, and 1 Hz, 2 Hz, 4 Hz...125 Hz for vibration. As the name “center” implies, it has some bandwidth (band), including the center frequency. For example, 1000Hz represents all sounds in the band from the lower frequency of 710Hz to the upper frequency of 1400Hz, centered at 1000Hz. The next band, 2000Hz, covers all frequencies without overlap, such as the lower frequency band of 1400Hz to the upper frequency band of 2800Hz centered on 2000Hz. The greater the center frequency, the greater the width of the octave band. The octave in octave band analysis refers to a 1/1-octave band, and a 1/3-octave band analysis is used when the bandwidth is divided more finely. In the case of vibration, 1/3 octave band analysis is often used.
JIS C 1513-1:2020 “Electroacoustics - Octave band and 1/N octave band filters (analyzers) - Part 1: Specifications” specifies the center frequency, lower frequency limit and upper frequency limit of 1/1 octave band as follows
- Center frequency: fm
- Upper limit frequency: fm×√(103/10)
- Lower limit frequency: fm/√(103/10)
The center frequency of the 1/3 octave band and the lower and upper frequency limits have the following relationship
- Center frequency: fm
- Lower limit frequency: fm/6√(103/10)
- Upper limit frequency: fm×6√(103/10)
Figure 3 Relationship between 1/1-octave band and 1/3-octave band
| 1/1 octave band | 1/3 octave band | 1/1 octave band | 1/3 octave band | ||||
| center frequency [Hz]. | bandwidth [Hz]. | center frequency [Hz]. | bandwidth [Hz]. | center frequency [Hz]. | bandwidth [Hz]. | center frequency [Hz]. | bandwidth [Hz]. |
| 1 | 0.71~1.41 | 0.8 | 0.71~0.89 | 125 | 89.1~178 | 100 | 89.1-112 |
| 1 | 0.89 to 1.12 | 125 | 112~141 | ||||
| 1.25 | 1.12~1.41 | 160 | 141~178 | ||||
| 2 | 1.41~2.82 | 1.6 | 1.41~1.78 | 250 | 178~355 | 200 | 178~224 |
| 2 | 1.78~2.24 | 250 | 224~282 | ||||
| 2.5 | 2.24~2.82 | 315 | 282~355 | ||||
| 4 | 2.82~5.62 | 3.15 | 2.82~3.55 | 500 | 355~708 | 400 | 355~447 |
| 4 | 3.55~4.47 | 500 | 447~562 | ||||
| 5 | 4.47~5.62 | 630 | 562~708 | ||||
| 8 | 5.62~11.2 | 6.3 | 5.62~7.08 | 1000 | 708~1413 | 800 | 708~891 |
| 8 | 7.08~8.91 | 1000 | 891~1122 | ||||
| 10 | 8.91~11.2 | 1250 | 1122~1413 | ||||
| 16 | 11.2~22.4 | 12.5 | 11.2~14.1 | 2000 | 1413~2818 | 1600 | 1413~1778 |
| 16 | 14.1~17.8 | 2000 | 1778~2239 | ||||
| 20 | 17.8~22.4 | 2500 | 2239~2818 | ||||
| 31.5 | 22.4~44.7 | 25 | 22.4~28.2 | 4000 | 2818~5623 | 3150 | 2818~3548 |
| 31.5 | 28.2~35.5 | 4000 | 3548~4467 | ||||
| 40 | 35.5~44.7 | 5000 | 4467~5623 | ||||
| 63 | 44.7~89.1 | 50 | 44.7~56.2 | 8000 | 5623~11220 | 6300 | 5623~7080 |
| 63 | 56.2~70.8 | 8000 | 7080~8913 | ||||
| 80 | 70.8~89.1 | 10000 | 8913~11220 | ||||
Examples of measures using octave analysis
Here is an actual example of our analysis and countermeasures using octave analysis. Factories that are called “specified factories” and have machinery that generates loud noise are regulated by the Noise Regulation Law in terms of the noise level at the boundary of the site. Since the criteria of the Noise Regulation Law are stricter at night, we found that the current condition (61 dBA) does not meet the regulatory standard of 50 dBA. As a result of octave band analysis, it was found that the sound between 125 Hz and 4k (4000) Hz (especially 250 Hz and 500 Hz) is loud, and that the regulation value of 50 dBA or less cannot be achieved without a significant reduction of sound in this band (see Figure 4). Soundproofing measures were taken (specifically, the location of the sound source in the building was changed, and equipment was vibration-proofed as a solid sound measure). ), the noise level at the site boundary was reduced from 61 dBA to 49 dBA, and as a result, the plant can now operate at night (see Figure 5).
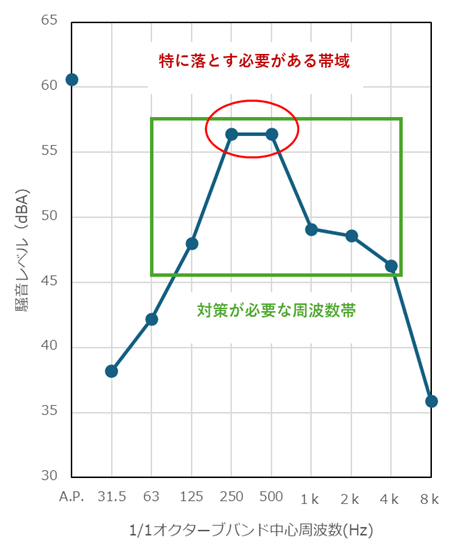Figure 4 1/1-octave band noise level at site boundary (before countermeasures)
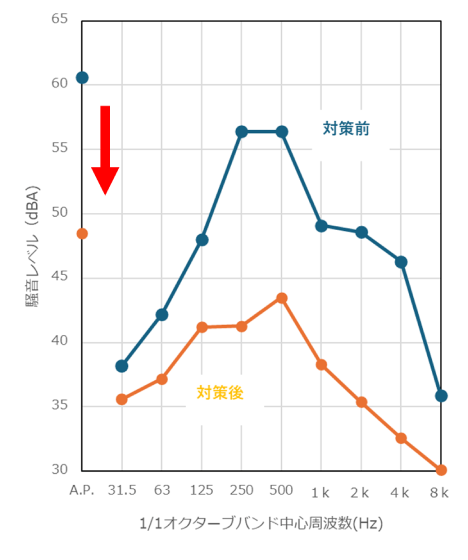
Figure 5: 1/1-octave band noise levels at site boundaries (before and after countermeasures)
As described above, octave band analysis is an effective analysis method for vibration and noise control.