When it comes to vibration damping, it is easy to get confused with various terms such as damping coefficient, damping constant, and damping ratio. Increasing damping is one of the basic concepts of vibration control, so it is necessary to understand it if you want to deepen your knowledge about vibration. Take this opportunity to clear your mind about damping.
What is attenuation?
When a force is input from the outside, the object begins to vibrate. The object continues to vibrate even after the input is removed, but it does not continue forever; it usually becomes smaller over time and eventually comes to rest due to air resistance, friction, heat, and other resistance that hinders vibration. This type of vibration is called damped vibration. As shown in Figure 1, in an undamped vibration system, the vibration does not decrease in size and continues forever (which is not possible in nature) even after the input has ceased to exist, but in a damped vibration system, the vibration decreases with time and converges.
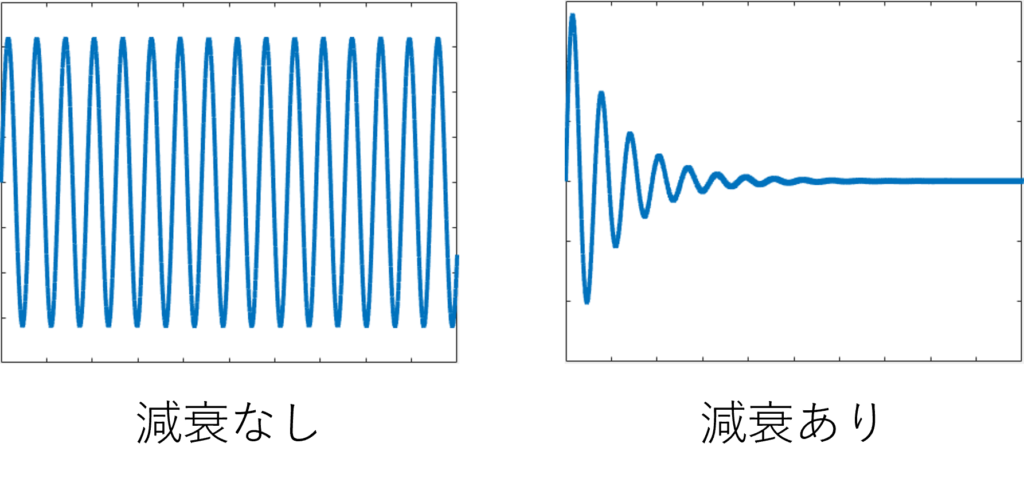
Figure 1: Image of the effect of damping (time axis waveform of vibration)
Attenuation magnitude expressions and terminology
Table 1 summarizes in an organized manner how the magnitude of attenuation is expressed and the terminology used.
When analyzing the damping effect, it is common to treat it as "viscous damping" where the resistance force is proportional to the velocity.
Table 1 List of Attenuation Terms
| terminology | symbol | unit | Description. |
|---|---|---|---|
| damping force | fd | [N] | Force to resist vibration In the case of viscous damping, it is proportional to the velocity of the vibration. fd=cv fdDamping force [N] c: Damping coefficient [N/m/s]. v: Velocity [m/s]. Damping coefficient" where the coefficient c on the velocity represents the degree of force to resist vibration. |
| attenuation coefficient | c | [N/m/s]. | |
| attenuation ratio | zeta | [None] | Damping coefficient for the critical state of oscillating or not oscillating (critical damping coefficient c)c) in the denominator and ζ = c/ccas a ratio of 0 to 1 (0 to 100%). In other words, the closer to 0, the less damping and the harder it is for the vibration to settle, and the closer to 1, the greater the damping and the faster the vibration settles. |
| decay constant | indecent | [None] | Same as damping ratio ζ Frequently used in the architectural field |
Damping ratios for building structures
Since damping is easily affected by environmental conditions such as the properties of the structure and materials, as well as temperature, it varies widely and is difficult to accurately determine. Therefore, it is difficult to determine an approximate value based on actual measurements and experiments. For example, the damping ratio for steel construction is 0.01 to 0.03, and for RC construction 0.02 to 0.04. Generally, 0.02 or 0.03 is used.
Relation between large and small damping ratios and vibration
Free vibration (vibration after input is lost)
Figure 2 shows how the free vibration waveform changes depending on the damping ratio ζ of the vibration system: the smaller ζ is, the longer the vibration continues, and the larger ζ is, the faster it converges. Furthermore, when ζ = 1, critical damping occurs, and the system converges without oscillation (reciprocating motion) when ζ exceeds this value.
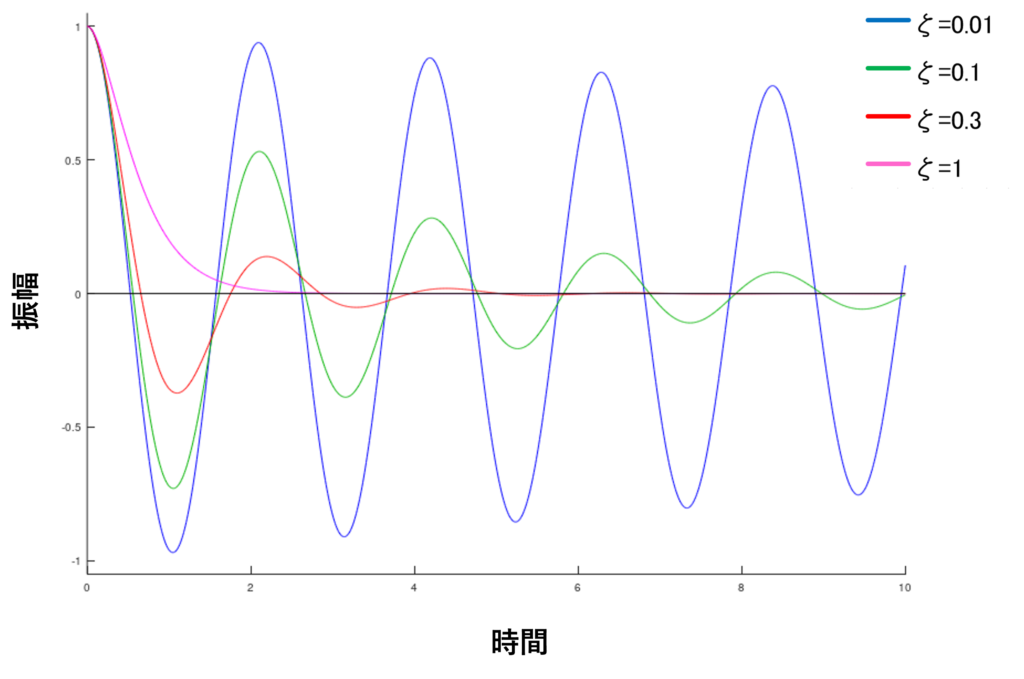
Figure 2 Comparison of free vibration waveforms by damping ratio
(2) Steady-state vibration (external force continues to be applied)
The horizontal axis in Figure 3 is the frequency ratio, which represents the ratio of the frequency of the input to the natural frequency of the vibrating system. The vertical axis is the amplitude ratio, which represents the amplification ratio relative to the input. In other words, the height of the peak when the horizontal axis is 1 represents the amplification of vibration when resonance occurs. As shown above, the smaller the value of ζ, the sharper the peak and the greater the amplification at resonance.
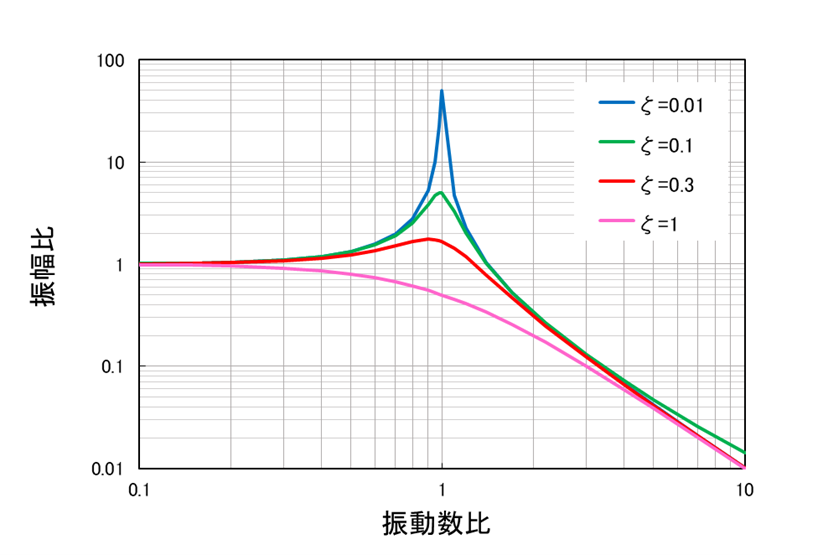
Figure 3 Comparison of resonance amplification by damping ratio
To increase vibration damping
A device that dampens vibration is called a damper, and there are various types depending on how the damping force is generated. Here are some typical examples.
- Viscous damper: Utilizes the viscous resistance of fluids such as liquids and gases.
- Friction damper: Utilizes frictional resistance due to sliding motion of metal or polymer materials.
- History damper: Utilizes the history characteristics of metallic materials and other materials due to repeated plastic deformation
- Mass damper: Damping force is provided by the inertial reaction force of a movable weight attached to the vibration system.
On the Construction Results page, you will find examples of (4) Mass Damper. Please take a look there as well!


