Walking, traffic vibration, wind, and other factors can cause floors and buildings to sway significantly, often due to a phenomenon called "resonance.
In this article, this "resonance" will be explained in an easy-to-understand manner.
What is resonance?
Resonance refers to a phenomenon in which, when force is applied to an object from the outside, the force is applied at a frequency equal to (close to) the "frequency at which the object tends to sway (natural frequency)," causing the sway to increase significantly. For example, on a pedestrian bridge, if the tempo (frequency) of walking (external force) matches the natural frequency, even a relatively small force can cause a large sway, just as one person walking on a pedestrian bridge may feel an uneasy sway.
Incidentally, when sound resonates instead of vibrating, it is called resonance.
What is natural frequency?
Let's start with the "natural frequency," which is indispensable for understanding resonance. Each object has its own unique oscillatory frequency (number of vibrations per second), and this frequency is called the "natural frequency.
When a force such as a tap is applied to an object, a natural frequency oscillation occurs immediately after the tap. The natural frequency depends on the shape and physical properties of the object. For example, the natural frequency of a stringed instrument such as a piano is determined by the length (ℓ) and tension (S) of the string, and when the string is struck, it vibrates at that natural frequency and sounds.
For reference, the natural frequency of a string is expressed by the formula
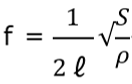
- f: Natural frequency [Hz] (number of vibrations per second)
- ℓ: Length of string [m].
- S: Tension [N] (force to pull the string)
- ρ: Line density [kg/m] (weight per meter of string)
As can be seen from this relationship, pianos and other instruments change their natural frequencies by adjusting the length and tension of the strings to express the do-re-mi scale.
Meaning of Resonance Curve
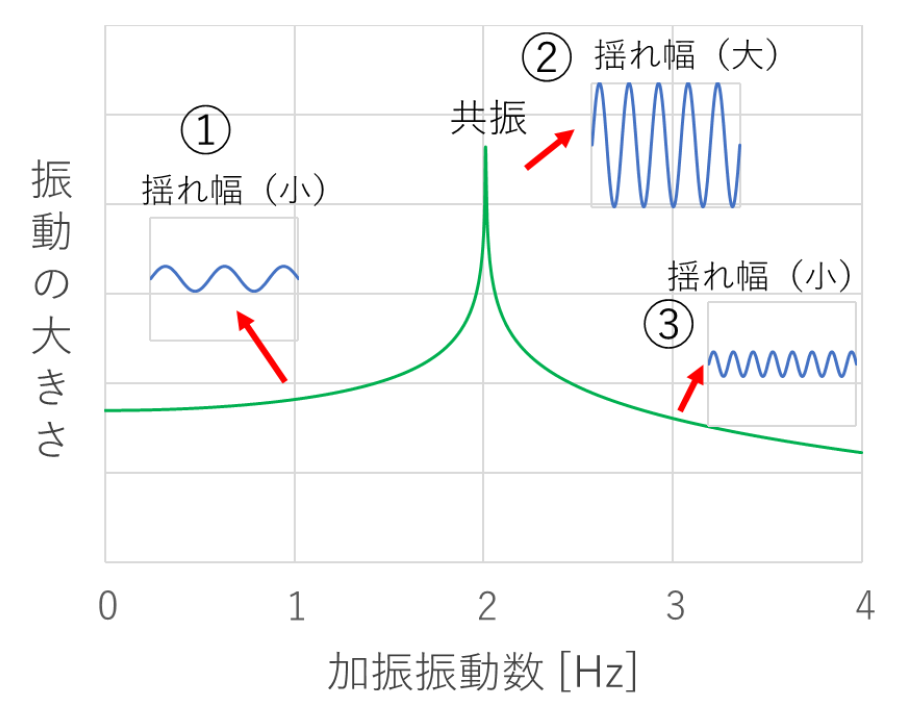
When the natural frequency of an object is 2 Hz (two vibrations per second), the relationship between the frequency of input vibration (Hz) and the magnitude of the resulting shaking is shown in Figure 1 and is called a resonance curve.
As the excitation frequency approaches the natural frequency (2 Hz), the shaking increases, reaching a maximum at the natural frequency. As the excitation frequency moves away from the natural frequency, the shaking becomes smaller.
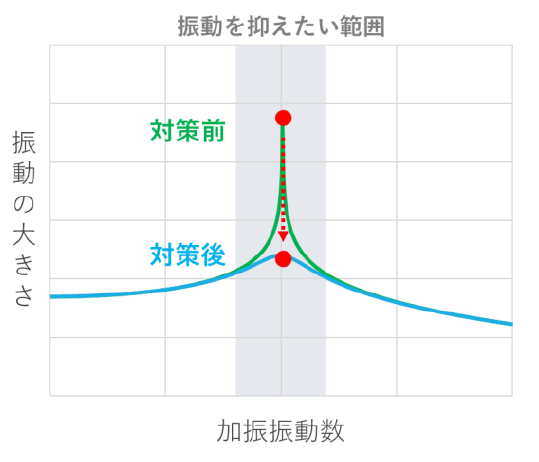
How to prevent increased vibration due to resonance
Resonance phenomena, in which even small forces cause large vibrations, can sometimes deteriorate occupant performance (comfort) and become a major problem. There are several ways to prevent this.
Take the case of resonance caused by floor swaying due to walking.
For example, assuming a walking tempo of 2 steps per second (2 Hz), a force with excitation force components at integer multiples of 2 Hz, such as 2 Hz, 4 Hz, and 6 Hz, is input to the floor (Figure 2). When the natural frequency of the floor and these excitation force components coincide, the floor resonates and shaking increases significantly.
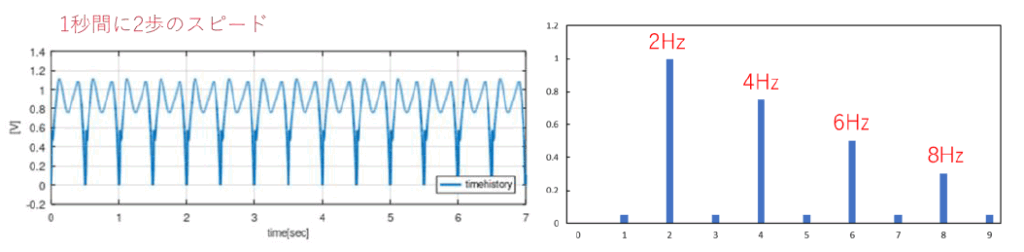
In this case, there are two typical measures to prevent resonance.
The first is to avoid matching the excitation frequency with the natural frequency of the floor (not to resonate).
The second method is to reduce the increase in sway due to resonance.
Specific measures
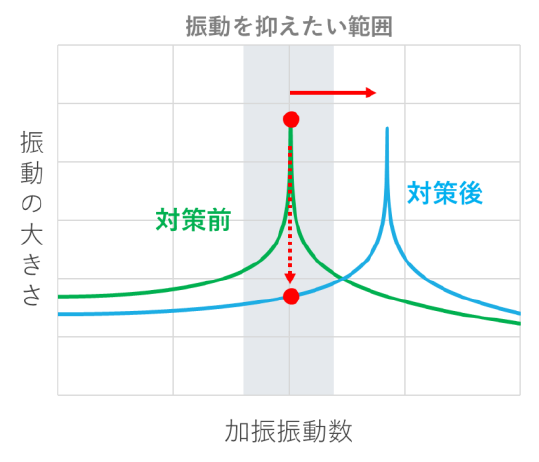
The first measure is to raise the natural frequency of the floor and shift it from the excitation frequency of walking to avoid resonance (Figure 3).
This method increases the rigidity of the structure and raises the natural frequency by increasing the size of the beams and the number of small beams.
Incidentally, resonance can also be avoided by lowering the natural frequency of the floor. However, lowering the natural frequency of the floor will make the floor more delicate (more prone to swaying). Even if resonance is avoided, the shaking itself may increase, and this is not a good method.
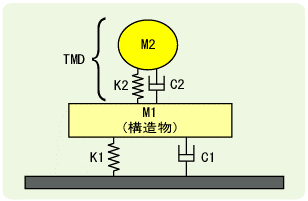
The second measure is to add damping, which reduces the amplification of shaking due to resonance and suppresses shaking (Figure 4).
Specifically, it is called a vibration control device.TMD (Tuned Mass Damper)and ... andAMD (Active Mass Damper)is placed on the floor and the weight of the vibration control device is shaken to absorb the floor shaking, thereby reducing the increase in shaking caused by resonance (Figure 5).