Vibration (vibration) control (damping) technology is used to reduce vibration (sway) in buildings and other structures in addition to vibration control technology used in earthquakes. This section focuses on vibration control and vibration control devices for environmental vibrations other than earthquakes. The lecture will provide an easy-to-understand explanation of the various types of vibration (shaking) that exist in our surroundings and what vibration control devices are effective for.
Cases where vibration control devices are effective
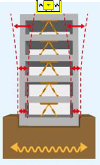
Introduction to Vibration Control (1)Seismic dampers, one of the vibration control devices introduced in Section 2.1, are only effective in large vibrations such as those caused by earthquakes. Therefore, the vibration control devices here are mainly mass dampers.
Mass dampers are effective against the natural frequencies of structures and the swaying around them, or resonance. Understanding this property is the key to effective use of vibration control technology.
Natural frequency and resonanceRelationship of
The frequency at which a structure is most likely to sway is called its natural frequency, expressed in units of [Hz] (hertz). At the natural frequency and its surrounding frequencies, the structure tends to sway easily, and even weak forces can cause it to sway greatly. This is called resonance.Resonance, the phenomenon of increased shaking - a comprehensive guide.(Please refer to the following table).
Example: Vibration of a pedestrian bridge
In the case of a pedestrian bridge, the typical natural frequency of vibration is that the bridge portion vibrates in the vertical direction as shown in Figure 1. Suppose the natural frequency of this pedestrian bridge is 3 Hz. The 3 Hz component of the force generated by vehicles passing on the road or people walking on the pedestrian bridge will cause the bridge to resonate, resulting in a large swaying motion. When crossing a pedestrian bridge, the uncomfortable fluffy swaying is often caused by resonant natural frequency swaying.
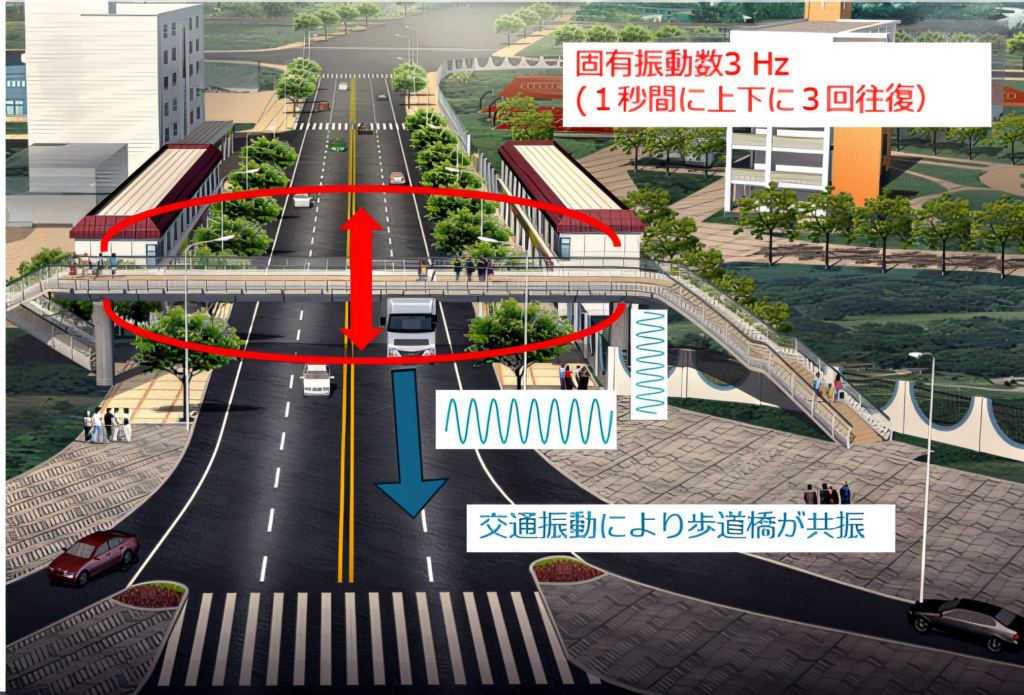
Figure 1 Example of resonance phenomenon
In the case of vibration problems caused by such resonance, the installation of mass dampers will likely reduce vibration and solve the problem.
Cases where mass damper is not effective
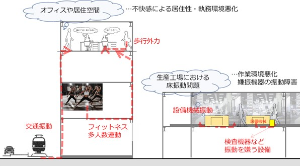
In general, most cases where vibration is a problem are caused by resonance, but some are not. In such cases, mass dampers are not expected to have much of a reduction effect.
Example: building vibration and electric drill vibration
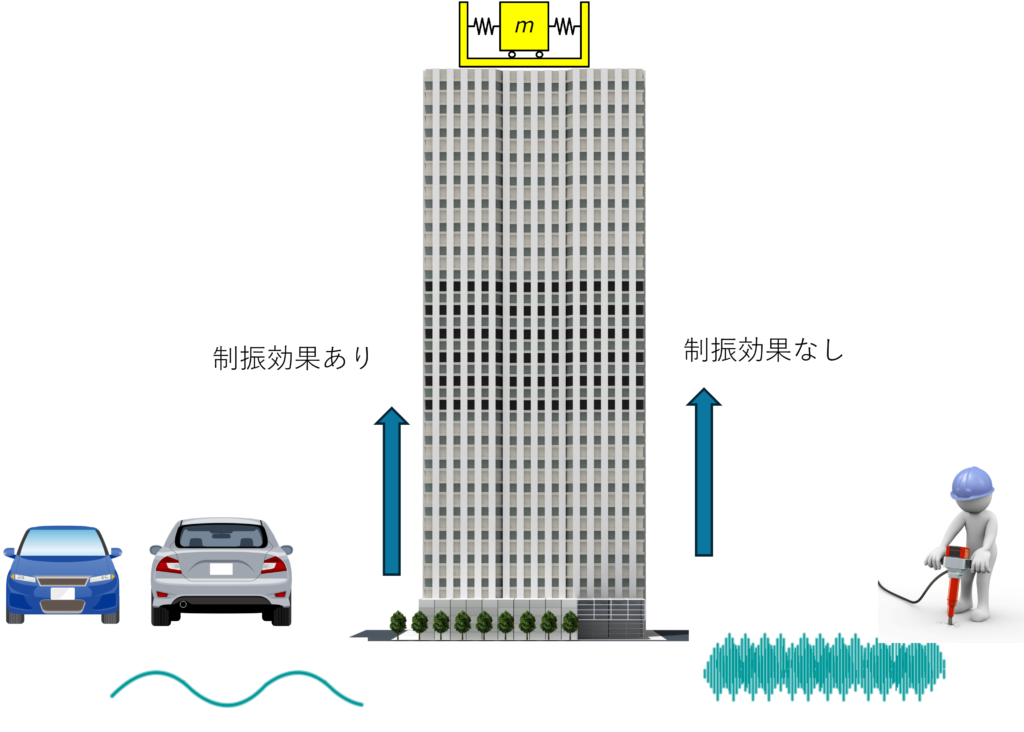
Figure 2 Relationship between Vibration Source and Vibration Damping Device
Consider a model in which a mass damper is installed on the roof to reduce the lateral sway of the entire building caused by road traffic vibration (let's assume a natural frequency of 1 Hz).
If traffic vibration, including vibration at the natural frequency of the building, is input from the ground, it will resonate at the natural frequency of the building and become a large vibration. In this case, mass dampers are effective.
On the other hand, the vibration component of the electric drill contains almost no vibration of the natural frequency of the building, so resonance does not occur. The higher frequency component of the electric drill's vibration is simply transmitted. For these non-resonant vibrations, vibration control devices are ineffective.
Frequency response characteristics of vibration
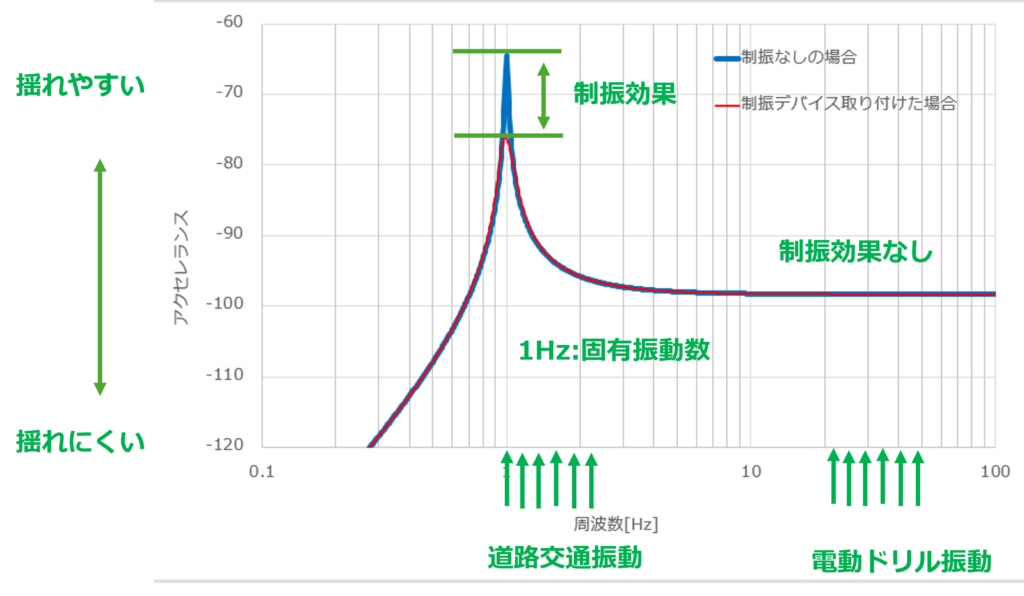
Figure 3 Building swayability and natural frequencies
The graph in Figure 3 is called the frequency response characteristics of vibration, and it shows the building's tendency to sway as described in the previous section, for each frequency. The frequency on the horizontal axis represents the period of shaking, with slow shaking on the left and faster shaking as one moves to the right. The vertical axis is a value representing the ease of shaking at each frequency, with larger values indicating greater ease of shaking.
The blue line shows the case of resonance without a mass damper, and the red line shows the case where a mass damper is installed. It can be seen that the installation of the damping device makes the area around 1 Hz, which was originally prone to shaking, a little less shaky. On the other hand, away from the peak, the blue and red lines overlap, showing no effect from vibration control.
Mass damper application examples
Mass dampers, TMDs and AMDs, can be applied to a wide range of vibrations, from minute tremors such as environmental vibrations to large tremors caused by strong winds or earthquakes. They can also be applied to both horizontal (lateral) and vertical (longitudinal) vibration.
TMDs are passive vibration control devices used to reduce structural sway.
AMDs are electrical vibration-damping devices that use active control. It requires a power supply and electrical components, and requires maintenance. However, it has the same vibration-damping effect as a TMD with approximately 10 times the weight, and can be installed in locations with limited load or installation area. It can also be effective for multiple natural frequencies.